Bạn đang xem bài viết Bất đẳng thức chebyshev là gì và những điều cần biết tại vfu2.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức chebyshev. Vậy bất đẳng thức chebyshev là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức chebyshev là gì?
Bất đẳng thức cộng Chebyshev được đặt theo tên nhà toán học Pafnuty Chebyshev. Được phát biểu rằng: Nếu cho
![]()
và
![]()
thì
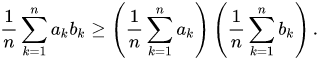
Tương tự, nếu
![]()
và
![]()
thì
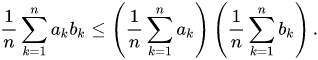
Chứng minh bất đẳng thức chebyshev
Bất đẳng thức cộng Chebyshev được chứng minh bằng cách dùng bất đẳng thức hoán vị.
Giả sử ta có hai chuỗi số được cho như sau
![]()
và
![]()
Vậy thì, theo bất đẳng thức hoán vị, ta có
![]()
là giá trị lớn nhất có thể sắp xếp được từ hai chuỗi số trên.
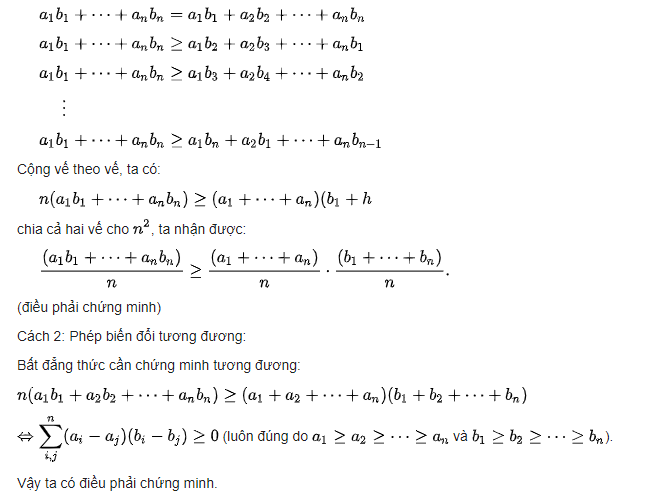
Bài tập ứng dụng bất đẳng thức chebyshev
Ví dụ 1 chebysev
$ dfrac a + b c + dfrac b + c a + dfrac c + a b geq 6 ( dfrac a ^ 2 + b ^ 2 + c ^ 2 ab + bc + ca) $ với $ 2b geq a + c $
Lời giải: Bất đẳng thức có dạng chebysev: $ (ab) ^ 2 ( dfrac c (a + b) -2ab ab) + (bc) ^ 2 ( dfrac a (b + c) -2bc bc + (ca) ^ 2 ( dfrac b ( c + a) -2ca ac) geq 0 $ (1)
Thứ tự các biến: giả sử: $ a geq b geq c $$ x = (ac) ^ 2, y = (bc) ^ 2, z = (ab) ^ 2 $ Dễ lấy: $ C_1 = dfrac a (b + c) -2bc bc, C_2 = dfrac b (a + c) -2ac ac, C_3 = dfrac c (a + b) -2ab ab $ Vậy phương trình cần chứng minh có dạng: $ C_1y + C_2x + C_3z geq 0 $ (2)
Ta sẽ chứng minh mệnh đề sau: $ C_1y + C_2x + C_3z geq (x + y + z) (C_1 + C_2 + C_3) $ (3) Theo tiêu chí 3 phần, chúng ta có phương trình trên đúng nếu và chỉ khi: $ 2y geq x + z $$ leftrightarrow dfrac 2b (a + c) -2ac ac – dfrac 2c (a + b) -2ab ab – dfrac 2a (b + c) -2bc bc $ $ leftrightarrow dfrac (2b-ac) (ab + bc + ca) abc geq 0 $ BĐT trên là đúng theo đề bài. Vậy (3) là đúng. Ta tiếp tục chứng minh rằng: $ ( x + y + z) (C_1 + C_2 + C_3) geq 0 $ In chứng thư: $ x + y + z geq 0 $ (làm $ x, y, z geq 0 $ và: $ C_1 + C_2 + C_3 = dfrac a ^ 2b + b ^ 2c + c ^ 2 a + b ^ 2a + c ^ 2b + a ^ 2c -6abc abc geq 0 $ (Theo AM-GM BDT) Từ trên ta có ĐPCM.
Ví dụ 2 chebysev
$ dfrac a + b c + dfrac b + c a + dfrac c + a b geq 6 ( dfrac a ^ 2 + b ^ 2 + c ^ 2 ab + bc + ca) $ với $ 2b geq a + c $
Lời giải: Bất đẳng thức có dạng chebysev: $ (ab) ^ 2 ( dfrac c (a + b) -2ab ab) + (bc) ^ 2 ( dfrac a (b + c) -2bc bc + (ca) ^ 2 ( dfrac b ( c + a) -2ca ac) geq 0 $ (1)
Thứ tự các biến: giả sử: $ a geq b geq c $$ x = (ac) ^ 2, y = (bc) ^ 2, z = (ab) ^ 2 $ Dễ lấy: $ C_1 = dfrac a (b + c) -2bc bc, C_2 = dfrac b (a + c) -2ac ac, C_3 = dfrac c (a + b) -2ab ab $ Vậy phương trình cần chứng minh có dạng: $ C_1y + C_2x + C_3z geq 0 $ (2)
Ta sẽ chứng minh mệnh đề sau: $ C_1y + C_2x + C_3z geq (x + y + z) (C_1 + C_2 + C_3) $ (3) Theo tiêu chí 3 phần, chúng ta có phương trình trên đúng nếu và chỉ khi: $ 2y geq x + z $$ leftrightarrow dfrac 2b (a + c) -2ac ac – dfrac 2c (a + b) -2ab ab – dfrac 2a (b + c) -2bc bc $ $ leftrightarrow dfrac (2b-ac) (ab + bc + ca) abc geq 0 $ BĐT trên là đúng theo đề bài. Vậy (3) là đúng. Ta tiếp tục chứng minh rằng: $ ( x + y + z) (C_1 + C_2 + C_3) geq 0 $ In chứng thư: $ x + y + z geq 0 $ (làm $ x, y, z geq 0 $ và: $ C_1 + C_2 + C_3 = dfrac a ^ 2b + b ^ 2c + c ^ 2 a + b ^ 2a + c ^ 2b + a ^ 2c -6abc abc geq 0 $ (Theo AM-GM BDT) Từ trên ta có ĐPCM.
Xem thêm:
Bất đẳng thức nesbit
Bất đẳng thức tam giác
Bất đẳng thức logarit
Cảm ơn bạn đã xem bài viết Bất đẳng thức chebyshev là gì và những điều cần biết tại vfu2.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Nguồn: https://reviewedu.net/bat-dang-thuc-chebyshev-la-gi-va-nhung-dieu-can-biet
Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức chebyshev. Vậy bất đẳng thức chebyshev là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức chebyshev là gì?
Bất đẳng thức cộng Chebyshev được đặt theo tên nhà toán học Pafnuty Chebyshev. Được phát biểu rằng: Nếu cho
![]()
và
![]()
thì
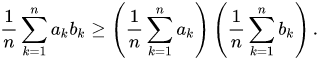
Tương tự, nếu
![]()
và
![]()
thì
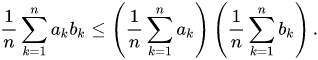
Chứng minh bất đẳng thức chebyshev
Bất đẳng thức cộng Chebyshev được chứng minh bằng cách dùng bất đẳng thức hoán vị.
Giả sử ta có hai chuỗi số được cho như sau
![]()
và
![]()
Vậy thì, theo bất đẳng thức hoán vị, ta có
![]()
là giá trị lớn nhất có thể sắp xếp được từ hai chuỗi số trên.
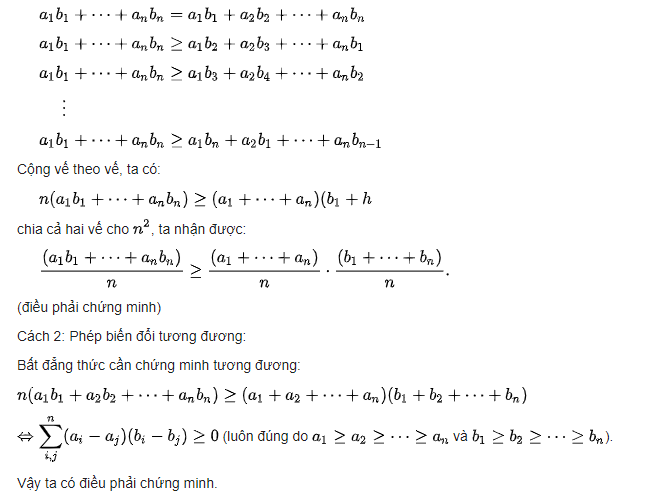
Bài tập ứng dụng bất đẳng thức chebyshev
Ví dụ 1 chebysev
$ dfrac a + b c + dfrac b + c a + dfrac c + a b geq 6 ( dfrac a ^ 2 + b ^ 2 + c ^ 2 ab + bc + ca) $ với $ 2b geq a + c $
Lời giải: Bất đẳng thức có dạng chebysev: $ (ab) ^ 2 ( dfrac c (a + b) -2ab ab) + (bc) ^ 2 ( dfrac a (b + c) -2bc bc + (ca) ^ 2 ( dfrac b ( c + a) -2ca ac) geq 0 $ (1)
Thứ tự các biến: giả sử: $ a geq b geq c $$ x = (ac) ^ 2, y = (bc) ^ 2, z = (ab) ^ 2 $ Dễ lấy: $ C_1 = dfrac a (b + c) -2bc bc, C_2 = dfrac b (a + c) -2ac ac, C_3 = dfrac c (a + b) -2ab ab $ Vậy phương trình cần chứng minh có dạng: $ C_1y + C_2x + C_3z geq 0 $ (2)
Ta sẽ chứng minh mệnh đề sau: $ C_1y + C_2x + C_3z geq (x + y + z) (C_1 + C_2 + C_3) $ (3) Theo tiêu chí 3 phần, chúng ta có phương trình trên đúng nếu và chỉ khi: $ 2y geq x + z $$ leftrightarrow dfrac 2b (a + c) -2ac ac – dfrac 2c (a + b) -2ab ab – dfrac 2a (b + c) -2bc bc $ $ leftrightarrow dfrac (2b-ac) (ab + bc + ca) abc geq 0 $ BĐT trên là đúng theo đề bài. Vậy (3) là đúng. Ta tiếp tục chứng minh rằng: $ ( x + y + z) (C_1 + C_2 + C_3) geq 0 $ In chứng thư: $ x + y + z geq 0 $ (làm $ x, y, z geq 0 $ và: $ C_1 + C_2 + C_3 = dfrac a ^ 2b + b ^ 2c + c ^ 2 a + b ^ 2a + c ^ 2b + a ^ 2c -6abc abc geq 0 $ (Theo AM-GM BDT) Từ trên ta có ĐPCM.
Ví dụ 2 chebysev
$ dfrac a + b c + dfrac b + c a + dfrac c + a b geq 6 ( dfrac a ^ 2 + b ^ 2 + c ^ 2 ab + bc + ca) $ với $ 2b geq a + c $
Lời giải: Bất đẳng thức có dạng chebysev: $ (ab) ^ 2 ( dfrac c (a + b) -2ab ab) + (bc) ^ 2 ( dfrac a (b + c) -2bc bc + (ca) ^ 2 ( dfrac b ( c + a) -2ca ac) geq 0 $ (1)
Thứ tự các biến: giả sử: $ a geq b geq c $$ x = (ac) ^ 2, y = (bc) ^ 2, z = (ab) ^ 2 $ Dễ lấy: $ C_1 = dfrac a (b + c) -2bc bc, C_2 = dfrac b (a + c) -2ac ac, C_3 = dfrac c (a + b) -2ab ab $ Vậy phương trình cần chứng minh có dạng: $ C_1y + C_2x + C_3z geq 0 $ (2)
Ta sẽ chứng minh mệnh đề sau: $ C_1y + C_2x + C_3z geq (x + y + z) (C_1 + C_2 + C_3) $ (3) Theo tiêu chí 3 phần, chúng ta có phương trình trên đúng nếu và chỉ khi: $ 2y geq x + z $$ leftrightarrow dfrac 2b (a + c) -2ac ac – dfrac 2c (a + b) -2ab ab – dfrac 2a (b + c) -2bc bc $ $ leftrightarrow dfrac (2b-ac) (ab + bc + ca) abc geq 0 $ BĐT trên là đúng theo đề bài. Vậy (3) là đúng. Ta tiếp tục chứng minh rằng: $ ( x + y + z) (C_1 + C_2 + C_3) geq 0 $ In chứng thư: $ x + y + z geq 0 $ (làm $ x, y, z geq 0 $ và: $ C_1 + C_2 + C_3 = dfrac a ^ 2b + b ^ 2c + c ^ 2 a + b ^ 2a + c ^ 2b + a ^ 2c -6abc abc geq 0 $ (Theo AM-GM BDT) Từ trên ta có ĐPCM.
Xem thêm:
Bất đẳng thức nesbit
Bất đẳng thức tam giác
Bất đẳng thức logarit






